![]() In this problem we will encounter the main physical features of dielectric spheres - their induced field and polarizability. The result is of great interest: understanding the interaction of light with small particles is one of the main concerns of nanophotonics. It leads to astonishing applications like cloaking, improvement of solar cells and lithography with extreme resolution.
In this problem we will encounter the main physical features of dielectric spheres - their induced field and polarizability. The result is of great interest: understanding the interaction of light with small particles is one of the main concerns of nanophotonics. It leads to astonishing applications like cloaking, improvement of solar cells and lithography with extreme resolution.
Problem Statement
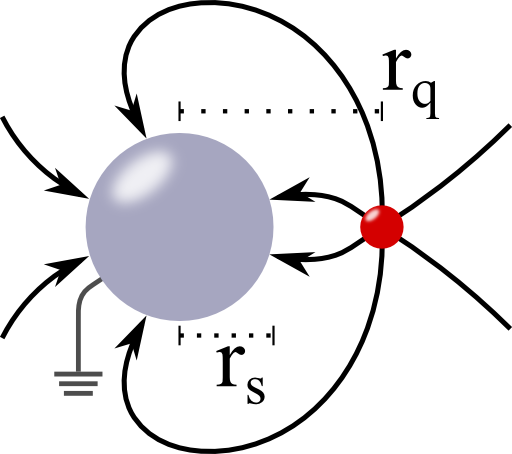 In the origin of the coordinate system is a metallic sphere with radius rs. At rq, there is a charge q. Calculate the resulting electrostatic potential for the cases if the sphere is grounded and if is isolated and charged with Qs. Calculate the surface charge density σ on the grounded sphere. You may want to proceed as follows:
In the origin of the coordinate system is a metallic sphere with radius rs. At rq, there is a charge q. Calculate the resulting electrostatic potential for the cases if the sphere is grounded and if is isolated and charged with Qs. Calculate the surface charge density σ on the grounded sphere. You may want to proceed as follows:
- Calculate the potential for the grounded sphere by the method of image charges and determine σ.
- How does your obtained potential has to be modified if the sphere is not grounded but at some fixed potential V?
- Relate the case of a fixed potential to that of an isolated charged sphere.
Background: "Ancient" and Modern Applications
A nice example for the field of a point charge in front of a charged metallic shell can be seen for example in the Van de Graaff generator. Everyone of us has seen these fancy images if someone gets charged by such a device and her/his hair follow the resulting field lines.
However, there are a lot of examples in modern science that make use of the results we are about to find. One of the main reasons is that the interaction of a charged body like an ion to a metallic sphere strongly depends on the distance between the two. We will see this both with respect to the magnitude and position of the image charge. This makes metallic spheres, or, generally, curved metallic nanoparticles a major candidate for sensor applications with a high spatial resolution. For more information I recommend the nice review article Plasmonic Materials, Advanced Materials 19, 2007 by Murray and Barnes.
Hints
In our problem, the surface charge density of the grounded sphere can be represented by a image charge q'. Where should this charge be situated regarding the symmetry of the configuration?
Solution
Let us first consider the case of the grounded sphere. From the rotational symmetry of the problem it becomes evident that the image charge we are looking for has to be placed on the connection line of the sphere's centre and the point charge. So we know that the electrostatic potential has the form
\[\phi\left(\mathbf{r}\right) = \begin{cases}\frac{q}{4\pi\epsilon_{0}}\left[\frac{1}{\left|\mathbf{r}-\mathbf{r}_{q}\right|}-\frac{\lambda}{\left|\mathbf{r}-\kappa\mathbf{r}_{q}\right|}\right] & r\geq r_{s}\\0 & r<r_{s}\end{cases}\]
where now λ = -q'/q and κ are dimensionless parameters characterizing the magnitude and the distance of the image charge to the origin in units of rq = |rq|, respectively. To determine the potential for the grounded sphere, we have to find the values of these parameters now.
Position and Magnitude of the Image Charge
We know that at |r| = rs, the electrostatic potential ф has to vanish.
Regarding the form of the potential, this implies
\[\begin{eqnarray*}\frac{1}{\left|r_{s}\mathbf{e}_{r}-\mathbf{r}_{q}\right|}-\frac{\lambda}{\left|r_{s}\mathbf{e}_{r}-\kappa\mathbf{r}_{q}\right|} & = & 0\ ,\ \mathrm{so}\\\frac{1}{r_{s}^{2}+r_{q}^{2}-2r_{s}r_{q}\cos\theta} & = & \frac{\lambda^{2}}{r_{s}^{2}+\kappa^{2}r_{q}^{2}-2\kappa r_{s}r_{q}\cos\theta}\ \mathrm{or}\\r_{s}^{2}+\kappa^{2}r_{q}^{2}-2\kappa r_{s}r_{q}\cos\theta & = & \lambda^{2}r_{s}^{2}+\lambda^{2}r_{q}^{2}-2\lambda^{2}r_{s}r_{q}\cos\theta\ .\end{eqnarray*}\]
We can see that with respect to the last 𝜃-term, κ = λ² must hold. Hence,
\[\begin{eqnarray*}r_{s}^{2}+\kappa^{2}r_{q}^{2} & = & \kappa r_{s}^{2}+\kappa r_{q}^{2}\ ,\\k^{2}-\left(1+\frac{r_{s}^{2}}{r_{q}^{2}}\right)+\frac{r_{s}^{2}}{r_{q}^{2}} & = & 0\ .\end{eqnarray*}\]
Remembering our good old highschool days we find the solutions of this equation as
\[\begin{eqnarray*}\kappa_{\pm} & = & \frac{1}{2}\left[1+\frac{r_{s}^{2}}{r_{q}^{2}}+\sqrt{\left(1+\frac{r_{s}^{2}}{r_{q}^{2}}\right)^{2}-4\frac{r_{s}^{2}}{r_{q}^{2}}}\right]=\frac{1}{2}\left[1+\frac{r_{s}^{2}}{r_{q}^{2}}\pm\left(1-\frac{r_{s}^{2}}{r_{q}^{2}}\right)\right]\\& = & \begin{cases}1 & +\ ,\\\left(r_{s}/r_{q}\right)^{2} & -\ .\end{cases}\end{eqnarray*}\]
We have used that the charge shall lie outside the sphere, so rs < rq. The solution where κ+ = 1, however, implies that the image charge is at the same position as q. This is formally correct but we may disregard this “zero-solution” here.
So, with \(k_{-}=\left(r_{s}/r_{q}\right)^{2}\):
- the image charge is positioned at \(\mathbf{r}_{m}=\left(r_{s}/r_{q}\right)^{2}\mathbf{r}_{q}\) and
- its magnitude is given as \(q^{\prime}=-\lambda q=-\left(r_{s}/r_{q}\right)q\).
Potential and Surface Charge Density: Grounded Sphere
Using the determined image charge, we can express the resulting potential as
\[\phi\left(\mathbf{r}\right) = \begin{cases}\frac{q}{4\pi\epsilon_{0}}\left[\frac{1}{\left|\mathbf{r}-\mathbf{r}_{q}\right|}-\frac{r_{s}/r_{q}}{\left|\mathbf{r}-\left(r_{s}/r_{q}\right)^{2}\mathbf{r}_{q}\right|}\right] & r\geq r_{s}\\0 & r<r_{s}\end{cases}\ .\]
We can see the dependence of the image charge on its position - the closer the charge is to the sphere rq → rs, the higher q'. However, the field far away weakens basically getting that of a dipole (see again The Electric Field of a Dipole). Remember on the contrary for example the case of a grounded plate. There, the image charge is always the negative of the q and does not depend on the distance.
Knowing this result, the derivation of the surface charge density is straight forward - it is given by the normal part of the displacement field D at the boundary of the sphere. So,
\[\begin{eqnarray*}\sigma\left(\theta\right) & = & -\epsilon_{0}\nabla\phi\left(\mathbf{r}=r_{s}\mathbf{e}_{r}\right)\cdot\mathbf{e}_{r}\\& = & \frac{q}{4\pi}\left(\frac{\mathbf{r}-\mathbf{r}_{q}}{\left|\mathbf{r}-\mathbf{r}_{q}\right|^{3}}-\frac{r_{s}}{r_{q}}\cdot\frac{\mathbf{r}-\left(r_{s}/r_{q}\right)^{2}\mathbf{r}_{q}}{\left|\mathbf{r}-\left(r_{s}/r_{q}\right)^{2}\mathbf{r}_{q}\right|}\right)_{\mathbf{r}=r_{s}\mathbf{e}_{r}}\cdot\mathbf{e}_{r}\\& = & \frac{q}{4\pi}\frac{r_{s}-r_{q}^{2}/r_{s}}{\left|\mathbf{r}_{s}-\mathbf{r}_{q}\right|^{3}}=-\frac{q}{4\pi r_{s}}\frac{r_{q}^{2}-r_{s}^{2}}{\left(r_{s}^{2}+r_{q}^{2}-2r_{s}r_{q}\cos\theta\right)^{3/2}}\ .\end{eqnarray*}\]
Note that the total charge on the sphere should equal q', since we could represent the potential with the image charge to fulfill the boundary conditions. We could verify this using
\[\nabla\cdot\mathbf{E}\left(\mathbf{r}\right)=\rho/\epsilon_{0}\]
or
\[q_{\mathrm{inside}}=\epsilon_{0}\int\mathbf{E}\left(\mathbf{r}\right)\cdot d\mathbf{A}\]
The situation, however is different if a charge is inside a metallic shell since inside the metal the electric field vanishes. Integrating over a Gaussian surface inside the shell thus yields that the induced charge (the integrated surface charge density) at the inside of the shell has to be the negative of the original charge, see again A Charge inside a Metallic Shell.
Constant Potential and the Isolated Sphere
If the sphere is held at a constant potential V, we simply have to add a term to the potential such that
\[\phi\left(\mathbf{r}=r_{s}\mathbf{e}_{r}\right)=V\]
This term has to fulfill the boundary conditions at |r| = ∞ and has to be a solution to the Poisson equation. Then, we have no choice but to let
\[\phi\left(\mathbf{r}\right) \rightarrow \phi\left(\mathbf{r}\right)+\frac{r_{s}V}{\left|\mathbf{r}\right|}\ .\]
Here we can see that the constant potential is equivalent to an additional charge qV of the sphere. By comparison to the point-charge potential we see that it is given by
\[q_{V} = 4\pi\epsilon_{0}r_{s}V\ .\]
This gives us the possibility to understand also the isolated sphere. Here, the charge Qs is constant, which corresponds, as we have just found out, to a constant potential.
Nonetheless, the free charge q induces the surface charge q'. By charge conservation, the total charge Qs has to be distributed between the image charge and qV, so
\[Q_{s}=q_{V}+q^{\prime} \mathrm{\ or\ } q_{V}=Q_{s}-q^{\prime}\ .\]
Hence, by the performed comparison we find that the potential of an isolated sphere with charge \(Q_{s}\) is given by
\[\begin{eqnarray*}\phi\left(\mathbf{r}\right) & = & \begin{cases}\frac{q}{4\pi\epsilon_{0}}\left[\frac{1}{\left|\mathbf{r}-\mathbf{r}_{q}\right|}-\frac{r_{s}/r_{q}}{\left|\mathbf{r}-\left(r_{s}/r_{q}\right)^{2}\mathbf{r}_{q}\right|}+\frac{Q_{s}/q+r_{s}/r_{q}}{\left|\mathbf{r}\right|}\right] & r\geq r_{s}\\\frac{1}{4\pi\epsilon_{0}}\frac{Q_{s}+\left(r_{s}/r_{q}\right)q}{r_{s}} & r<r_{s}\end{cases}\ .\end{eqnarray*}\]
Again, the first term for r ≥ rs corresponds to the point charge, the second to the induced one and the last one to the constant charge of the isolated sphere.
As you can see, by simple application of the method of image charges we were able to find the electrostatic potential of the metallic sphere subject to a point charge. This problem would have been much more complicated as you might imagine simply from the solution we have just derived!